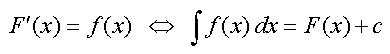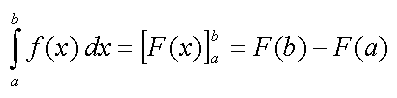Navigation:
 

DAS BESTIMMTE INTEGRAL

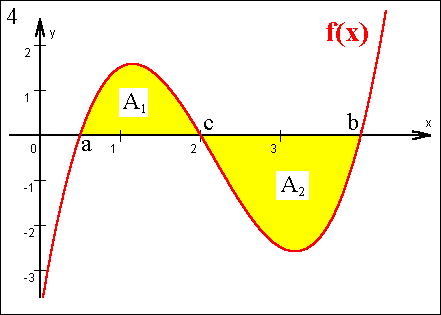
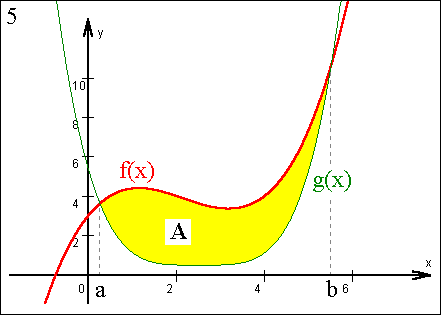
Ausgangspunkt für die "Erfindung" der Integralrechnung war das Bedürfnis, die Fläche unter einer stetigen Funktion zu berechnen (Bild 1). Geht man von der Funktionsgleichung aus, ist es mittels verschiedener Verfahren (z.B. Differentialrechnung) möglich, den Kurvenverlauf relativ genau zu bestimmen. Kennt man die Begrenzungen der Fläche, könnte man ihren Inhalt z.B. durch Auszählen von Kästchen einigermaßen genau ermittel. Auch ausgebildete Mathematiker gehen (fast) so vor.

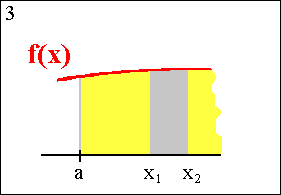
In Bild 2 ist die Zerlegung der Fläche in gleich breite Streifen angedeutet. Betrachten wir nun einen solchen Streifen unter dem Mikroskop:

Die Fläche des beliebig ausgewählten grauen Streifens ist fast rechteckig und kann deshalb durch die Formel 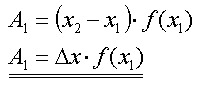näherungsweise berechnet werden. Man müßte sich nun die Mühe machen, die Flächen aller Streifen einzeln zu berechnen, um anschließend die Summe zu bilden. Von großer Bedeutung ist die Feststellung, daß die Genauigkeit des Endergebnisses von der Breite bzw. von der Anzahl der Streifen abhängig ist: je schmaler, desto genauer.

Wer in der Schule gelegentlich mitgedacht hat, vermutet nun bestimmt, daß wir uns mit Näherungswerten nur ungern zufriedengeben. Die exakte Flächenberechnung erfordert aber, daß man die Anzahl der Streifen ins Unendliche wachsen läßt. Das heißt, daß die Streifen unendlich schmal sein müssen. Leider sind dann "normale" Rechnungen mit "normalen" Zahlen nicht mehr möglich. Ohne Kenntnisse über Zahlenfolgen und deren Grenzwerte besteht keine Möglichkeit, die Flächenberechnung mit einem genauen Endergebnis abzuschließen.

Glücklicherweise haben findige Mathematiker eine Abkürzung entdeckt, wodurch man beliebige Flächen ohne den Umweg über einen Grenzwert berechnen kann. Dazu im dritten Abschnitt mehr. Zunächst sollte man lediglich den "Ansatz" zur Kenntnis nehmen, der uns zukünftig Maßzahlen für Flächen wie in Bild 1 liefert - das bestimmte Integral: 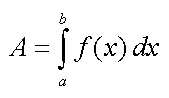Dabei sind a und b die beiden Integrationsgrenzen (a < b) und f(x) ist die die Fläche begrenzende stetige Funktion. Über die Buchstabenkombination dx sollten wir uns im Unterricht unterhalten.

Wie bestimmte Integrale konkret berechnet werden, möchte ich hier noch nicht verraten - aber folgende Sonderfälle sollten man schon verstehen:

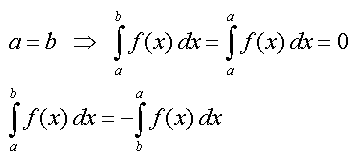DAS UNBESTIMMTE INTEGRAL

Lassen wir doch die Integrationsgrenzen a und b des bestimmten Integrals erst einmal einfach weg. Passend zur Ausgangsfunktion f(x) definieren wir eine Stammfunktion F(x), so daß gilt:

Was steckt hinter dieser Formel ? 1.) Die Ableitung der Stammfunktion F ergibt die Ausgangsfunktion f. 2.) Wenn man f integriert, erhält man eine von mehreren möglichen Stammfunktionen F. 3.) Alle Stammfunktionen haben dieselbe Form - sie unterscheiden sich nur an der letzten Stelle durch den x-freien Summanden. Daher erscheint "c" als Platzhalter für einen konstanten Summanden in obiger Gleichung.

Folgende fundamentale Erkenntnis sollte nunmehr herangereift sein : Die Integralrechnung ist die Umkehrung der Differentialrechnung.

Anhand von Integrationsregeln kann man Stammfunktionen schnell und recht einfach berechnen - Beispiele dazu findet man natürlich auch auf dieser Seite. Ausdrücklich hinweisen möchte ich auf die Tatsachen, daß konstante Faktoren beim Integrieren beibehalten ("durchgeschleift") werden können, und daß man mehrere Summanden eines Integrals getrennt integrieren kann:

DER HAUPTSATZ DER DIFFERENTIAL- UND INTEGRALRECHNUNG

Dieser Hauptsatz ermöglicht die Berechnung bestimmter Integrale mit Hilfe einer Stammfunktion, von der bisher nur im Zusammenhang mit unbestimmten Integralen die Rede war. Auf den Beweis des Satzes möchte ich zunächst verzichten

Bei der bedenkenlosen Anwendung der Flächenformel entstehen jedoch gelegentlich Probleme. So erhalten zum Beispiel Flächen unterhalb der x-Achse plötzlich ein negatives Vorzeichen - doch was hat das zu bedeuten ? Weiterhin kann es passieren, daß deutlich sichtbare Flächen den Inhalt Null haben, wenn sie aus mehreren Teilflächen bestehen. Kein Problem für den Mathematiker, der solche Sonderfälle als "orientierte Flächen" bezeichnet und die Lösungen damit akzeptiert. Manche Menschen möchten jedoch die Maßzahl der wirklich sichtbaren, absoluten Fläche kennen. Ihnen kann geholfen werden: Der absolute Betrag (daher die Bezeichnung "absolute Fläche") macht also alles wieder gut und sollte daher stets verwendet werden!

Das Problem der Teilflächen löst man übrigens einfach dadurch, daß man abschnittsweise integriert. Teilflächen entstehen z.B. immer dann, wenn die zu integrierende Funktion f(x) im Integrationsintervall eine oder mehrere Nullstellen hat. Diese müssen also zuvor berechnet werden. Natürlich kommt einer zuverlässigen Skizze erhöhte Bedeutung zu. Im folgenden Bild 4 hat f(x) im Integrationsintervall die Nullstelle c:

Zur Berechnung der Gesamtfläche (absolute, sichtbare Fläche) berechnet man zunächst alle relevanten Nullstellen und verfolgt dann den Ansatz

Abschließend sei noch darauf hingewiesen, wie die zwischen zwei Funktionen eingeschlossene Fläche berechnet werden kann:

Die Integrationsgrenzen (Schnittstellen) bestimmt man übrigens durch das Gleichsetzen der Funktionsgleichungen. Wenn man sich nun vorstellt, daß die Größe dieser Fläche vom Abstand beider Funktionen abhängig ist, fällt es nicht schwer, den hier zu verwendenden Ansatz zu verstehen:

Viel Spaß beim Üben !