
e - Funktionen
Da geht's doch schon los ... Wie soll man das rechnen ?
Ich empfehle eine grafische Überlegung, denn ausgehend von der umgestellten Gleichung kann man sich die Bilder der Teilfunktionen leicht beschaffen:
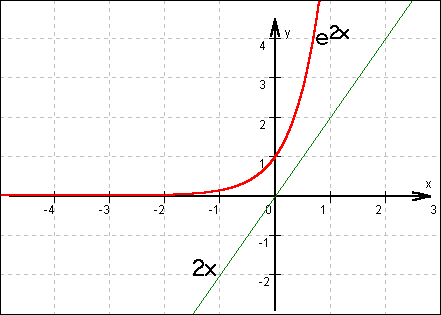
Da es keine Schnittpunkte gibt, kann f(x) keine Nullstellen haben.
und Nachweis
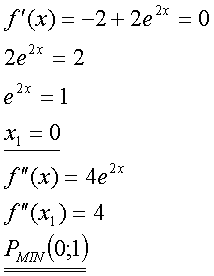
Wenn eine Potenz von e gleich 1 sein soll, muß der Exponent Null sein.
Diese Gleichung hat keine Lösung, denn eine Potenz von e wird niemals Null!. Einen Wendepunkte kann es also nicht geben.
Im positiv Unendlichen dominiert die e-Funktion. f(x) wird dort also auch ins Unendliche steigen. Im negativ Unendlichen nähert sich die e-Funktion der Null an, aber der Summand -2x ist unendlich groß.
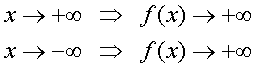
Die e-Funktion wächst stärker als jede Potenz von x!
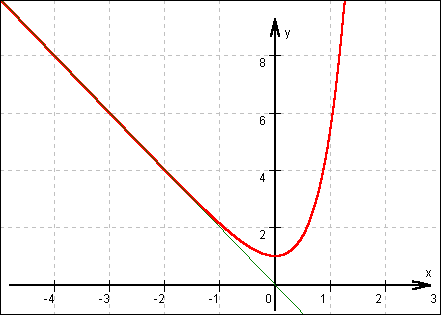
Man sollte noch einige Punkte von Hand berechnen, das erhöht die Genauigkeit der Skizze.