e - Funktionen
     
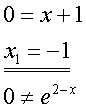
  Nullstellen  Wir setzen f(x) gleich Null und betrachten beide Faktoren der Gleichung nacheninander:
kleiner Tip am Rande :
Eine Potenz von e wird niemals Null!
Extrempunkt 
und Nachweis		 kleiner Tip am Rande :
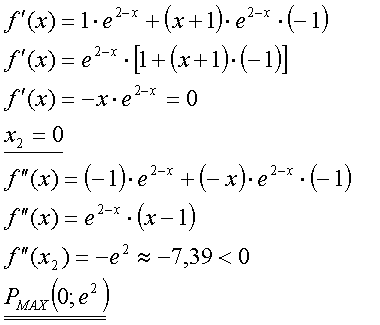
Siehe oben. Wieder werden beide Faktoren der Ableitung getrennt betrachtet.
Wendepunkt
Verhalten im Unendlichen Die e-Funktion wächst stärker als jede Potenz von x!
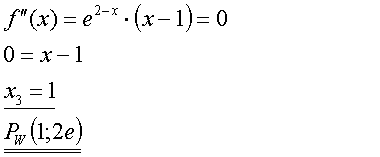
Folglich verhält sich f(x) im Unendlichen wie die klassische e-Funktion - nur ein wenig seitenverkehrt (wegen -x im Exponenten): Sie nähert sich der Null an. Im negativ Unendlichen sorgt der Faktor (x+1) für negativ unendlich große Werte:
Graph kleiner Tip am Rande :
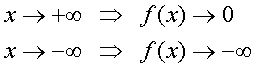
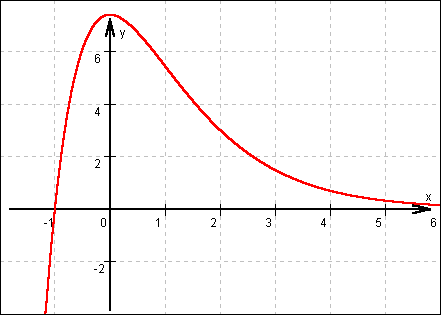
Man sollte noch einige Punkte von Hand berechnen, das erhöht die Genauigkeit der Skizze.
Post an mich 
Startseite
honich.de