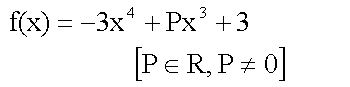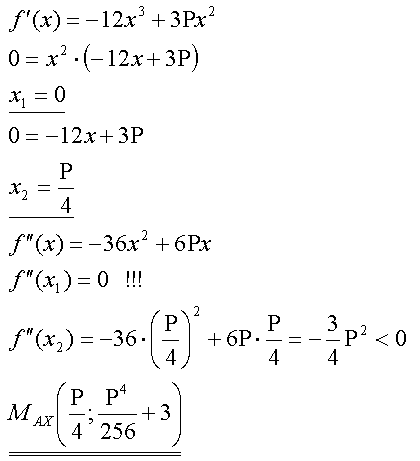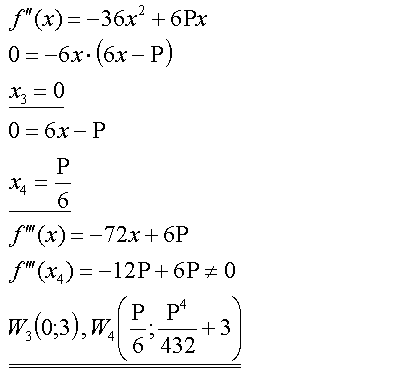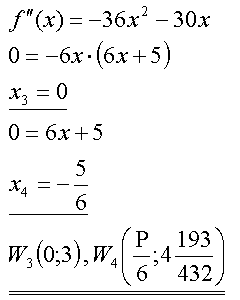ganzrationale Funktionen
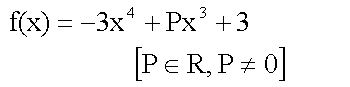		Wie man sieht, ist der Kurvenverlauf von einem Parameter P abhängig. Es ist zunächst zu untersuchen, welchen Einfluß P auf das Vorhandensein und die Lage von Extrem- und Wendepunkten hat. Auf die Berechnung der Nullstellen wird verzichtet.
	Def.-Bereich	Der Definitionsbereich umfaßt die Menge aller reellen Zahlen. f(x) ist überall stetig.
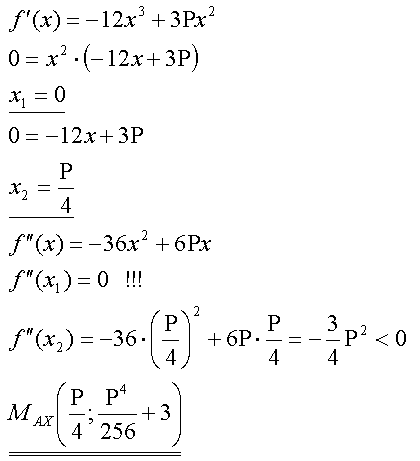
	Extrempunkte  und Nachweis	Beim Ableiten ist P als Konstante (d.h. wie eine ganz "normale" Zahl) zu behandeln. Die Lage des Punktes MAX ist also direkt von P abhängig. MAX hat aber in jedem Fall eine positive y-Koordinate.	Randbemerkung:   Die erste Lösung konnte anhand der zweiten Ableitung nicht als Extrempunkt bestätigt werden.
	Wendepunkte und Nachweis	Einen Wendepunkt (Sattelpunkt) vermuten wir bereits an der Stelle x = 0.	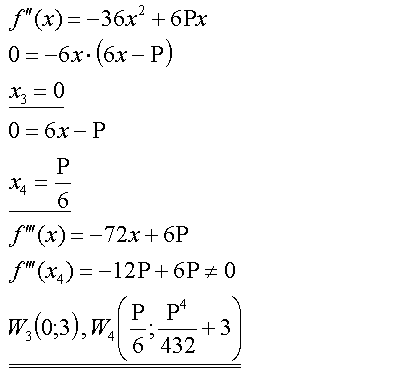Randbemerkung:   Wie jeder weiß, wird ein Produkt Null, wenn einer der Faktoren dieses tut. Folglich untersucht man sie beide nacheinander (genau wie eben).
	Verhalten im Unendlichen	Anhand des negativen Koeffizienten der hochsten Potenz von x erwarten wir eine nach unten geöffnete Kurve 4. Grades.
	P = -5	Zwecks besserer Veranschaulichung wird nun P genau definiert. Die anhand der eben gemachten Berechnungen darzustellende Funktion hat damit die Gleichung
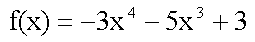	Extrempunkt	Wiederholen wir die Rechnung von oben: Das entspricht der schon bekannten allgemeinen Lösung.
	Wendepunkte	Auch hier sind keine Überraschungen zu erwarten:
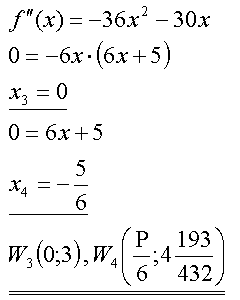	Graph	Im Bild wird nun f(x) mit P = -5 hervorgehoben dargestellt. Den Einfluß des Parameters macht man sichtbar, indem er in ganzen Schritten von -5 bis +5 geändert wird. Das Ergebnis ist eine Kurvenschar.

 

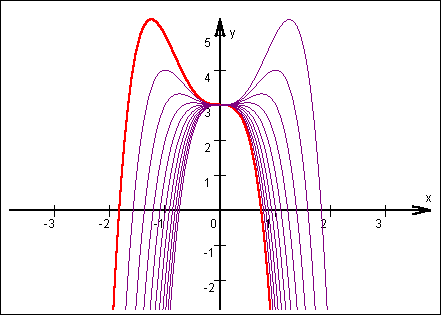Post an mich	Startseite	honich.de