
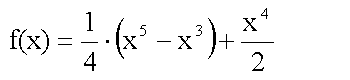
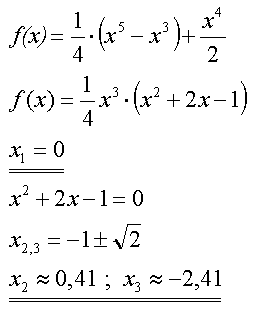
Ist es aufgefallen ? Die erste Lösung steht für eine dreifache Nullstelle !
und Nachweis
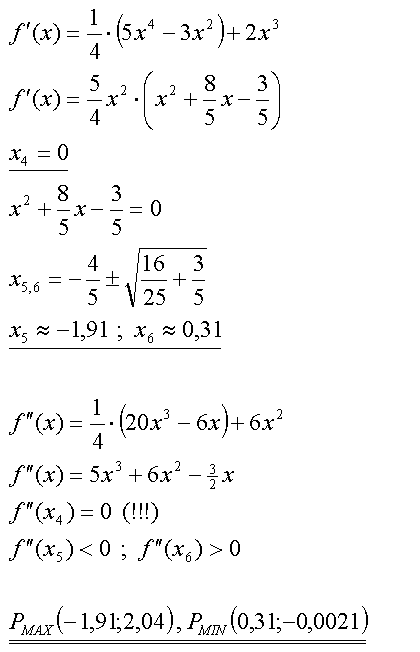
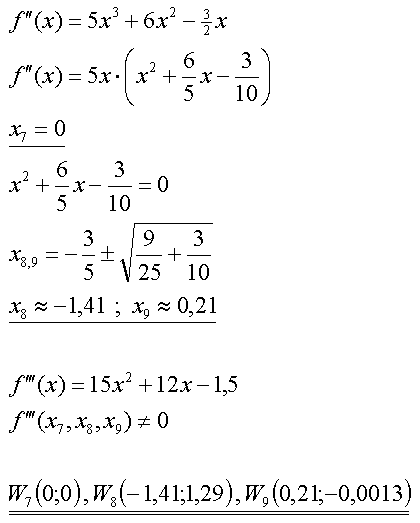
Bitte nicht schwach werden: Einige Funktionswerte gehören zum Bereich der "komischen Zahlen" (K). Der Sattelpunkt hat sich übrigens bestätigt!
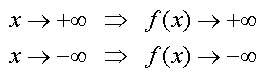
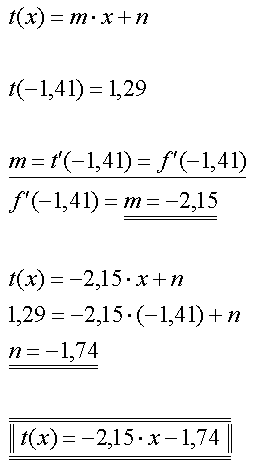
 |
|||
| ganzrationale Funktionen | |||
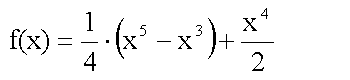 |
|||
| Das sieht aber kompliziert aus ! Und damit es so richtig schwer wird, suche ich eine Wendetangente t(x) gleich noch dazu. Das Bild von f(x) und t(x) soll im Intervall [-2,5;+1,5] gezeichnet werden. | |||
| Def.-Bereich | Bei einer ganzrationalen Funktion ist es nicht anders zu erwarten: Der Definitionsbereich umfaßt die Menge aller reellen Zahlen. f(x) ist überall stetig. | ||
| Nullstellen | Vor dem Rechnen sollten wir uns zuerst über das Erscheinungsbild
der Funktionsgleichung Gedanken machen - der Rest geht dann von alleine.
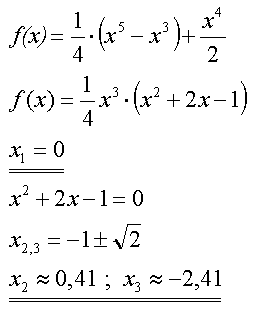
Ist es aufgefallen ? Die erste Lösung steht für eine dreifache Nullstelle ! |
Randbemerkung: Durch Ausklammern erzeugt man ein Produkt. Jeder Faktor davon wird nacheinander gleich Null gesetzt. | |
| Extrempunkte
und Nachweis |
Immer noch geht nichts ohne die erste Ableitung...
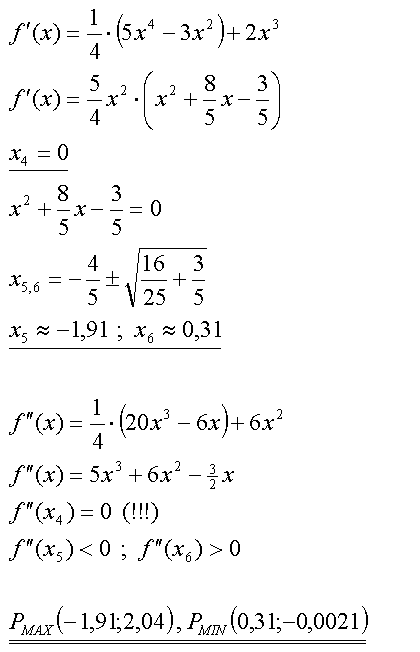 |
Randbemerkung: Die erste Lösung konnte anhand der zweiten Ableitung nicht als Extrempunkt bestätigt werden. | |
| Wendepunkte und Nachweis | An der Stelle x = 0 müssen wir mit einem Sattelpunkt rechnen.
Mal sehen, ob's stimmt:
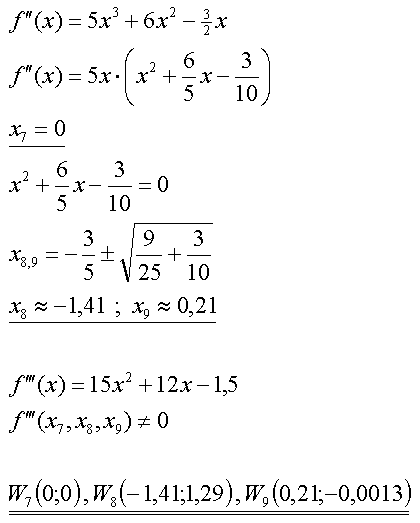
Bitte nicht schwach werden: Einige Funktionswerte gehören zum Bereich der "komischen Zahlen" (K). Der Sattelpunkt hat sich übrigens bestätigt! |
Randbemerkung: Wie jeder weiß, wird ein Produkt Null, wenn einer der Faktoren dieses tut. Folglich untersucht man sie beide nacheinander (genau wie eben). | |
| Verhalten im Unendlichen | Von einer ganzrationalen Funktion fünften Grades ohne negativen
Koeffizienten der höchsten Potenz hat man die Vorstellung, daß
sie "irgendwie von links unten nach rechts oben" verläuft und dazwischen
die Monotonie wechseln kann. Mathematisch gesagt:
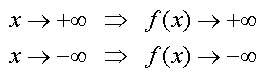 |
||
| Wendetangente | Anhand der Daten entscheide ich mich für Wendepunkt W8, um dort
eine Tangente anzulegen. Man will schließlich auch etwas erkennen
können. Wie lautet die Tangentengleichung ? Wir sehen nun die
allgemeine Form und suchen nach den Merkmalen der Gerade:
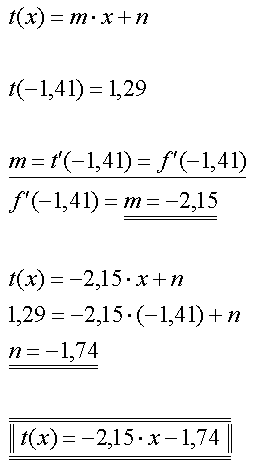 |
Randbemerkung: Die Tangentengleichung ist die Gleichung einer Gerade. Diese hat zwei Unbekannte - m und n. Die Steigung m errechnet sich aus der Tatsache, daß f(x) und t(x) im Berührungspunkt gleich steil sind - und für die Steilheit von f(x) hat man ja schon f'(x) berechnet. In die Ableitung wird nur noch die x-Koordinate des Wendepunktes eingesetzt. So geht es weiter: In die halb fertige Tangentengleichung setzt man nun noch die x- und die y- Koordinate des Wendepunktes ein, um n zu berechnen. | |
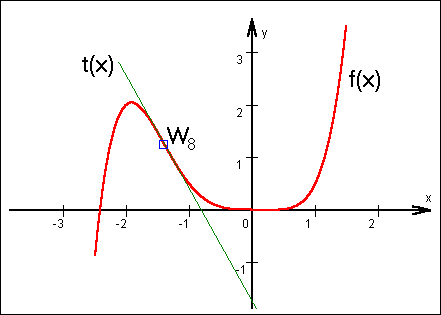
| Graph | f(x) und t(x) stellen sich nun wie folgt dar:
 |
||
Post an mich |
Startseite |
honich.de |