 |
|||
| gebrochen-rationale Funktionen | |||
 |
|||
| Def.-Bereich, Stetigkeit | Betrachten wir zunächst den Nenner:
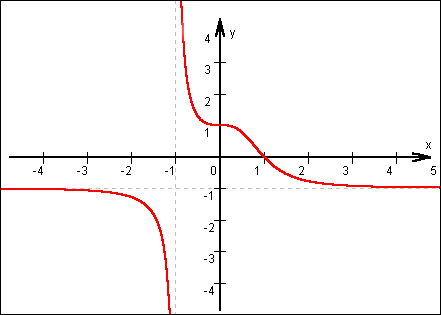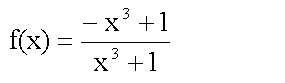
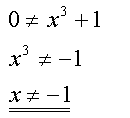
f(x) ist also an der Stelle x = -1 unstetig.
|
kleiner Tip am Rande: Auch wenn der Taschenrechner die dritte Wurzel aus einer negativen Zahl nicht ziehen kann - es gibt sie wirklich! | |
| Nullstellen | Weiter geht es mit der Untersuchung des Zählers:
 |
||
| Extrempunkte
und Nachweis |
Die Quotientenregel liefert uns die erforderlichen Ableitungen:
Demnach ist unser Extrempunkt gar kein Extrempunkt! Aber was dann? |
kleiner Tip am Rande: Bekanntlich reicht es aus, wenn man hier nur den Zähler untersucht. Der Nenner ist ja schon erledigt... | |
| Wendepunkte | Betrachten wir zunächst die zweite Ableitung etwas genauer:
Gemeinsam mit den Erkenntnissen der Extrempunktberechnung wissen wir nun, daß es sich beim Punkt (0;1) um einen Sattelpunkt handelt. Auf den Nachweis der Wendepunkte wird verzichtet. |
kleiner Tip am Rande: Wie jeder weiß, wird ein Produkt Null, wenn einer der Faktoren dieses tut. Folglich untersucht man sie beide nacheinander. | |
| Verhalten im Unendlichen | Wichtige Schlußfolgerungen kann man ziehen, wenn man den Funktionsterm
als Summe schreibt:
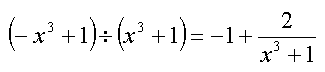
Der ganze Anteil der Summe liefert uns die waagerechte Asymptote y = -1. |
kleiner Tip am Rande: Das zugrundeliegende Verfahren heißt "Polynomdivision"! | |
| Graph | Da wir nur drei Punkte berechnet haben, kommt den Asymptoten eine besondere
Bedeutung zu. Sie bestimmen den Kurvenverlauf wesentlich mit.
 |
||
 |
 |
 |
 |
Post an mich |
Startseite |
honich.de |