 |
|||
| gebrochen-rationale Funktionen | |||
 |
|||
| Def.-Bereich, Stetigkeit | Betrachten wir zunächst den Nenner:
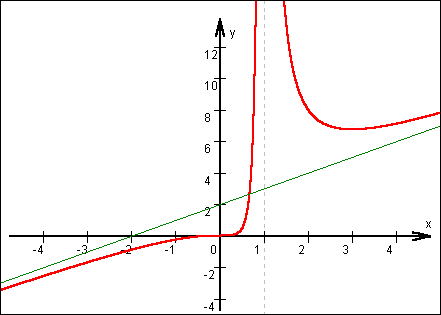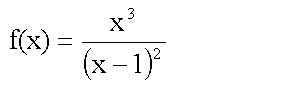
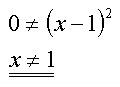
f(x) ist also an der Stelle x = 1 unstetig.
|
||
| Nullstellen | Ich will nicht lange um den heißen Brei herumreden:
Bei x = 0 dürfen wir mit Sicherheit eine Nullstelle erwarten. |
||
|
Extrempunkte und Nachweis |
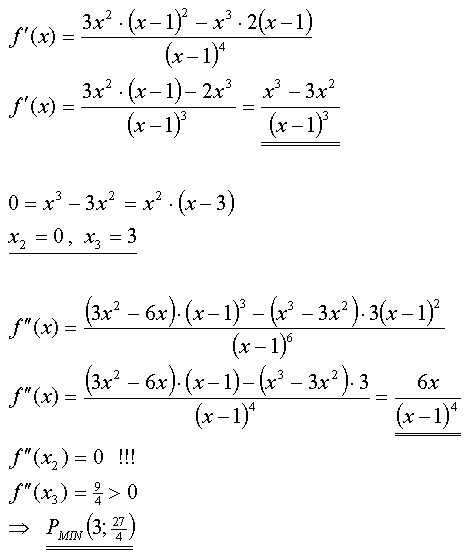
Die erste Lösung (x = 0) deutet auf etwas Besonderes hin! |
kleiner Tip am Rande: Auch hier rechnet man mit der Quotientenregel und untersucht nur den Zähler. Der Nenner ist ja schon erledigt... | |
| Wendepunkt | Betrachten wir zunächst die zweite Ableitung etwas genauer:
Gemeinsam mit den Erkenntnissen der Extrempunktberechnung wissen wir nun, daß es sich beim Punkt (0;0) um einen Sattelpunkt handelt. Auf den Nachweis der Wendepunkte wird verzichtet. |
kleiner Tip am Rande: In solch einfachen Fällen kann man auf den Rechenweg verzichten. | |
| Verhalten im Unendlichen | Wichtige Schlußfolgerungen kann man ziehen, wenn man den Funktionsterm
als Summe schreibt:
Der ganze Anteil der Summe liefert uns die Asymptote y = x + 2. |
kleiner Tip am Rande: Das zugrundeliegende Verfahren heißt "Polynomdivision"! | |
| Graph | Da wir nur drei Punkte berechnet haben, kommt den Asymptoten eine besondere
Bedeutung zu. Sie bestimmen den Kurvenverlauf wesentlich mit.
 |
||
 |
 |
 |
 |
Post an mich |
Startseite |
honich.de |