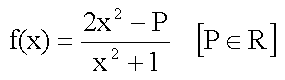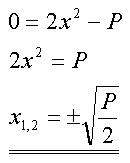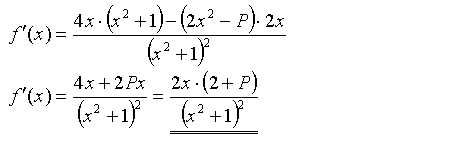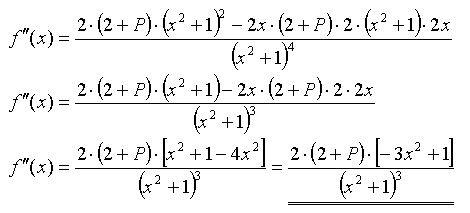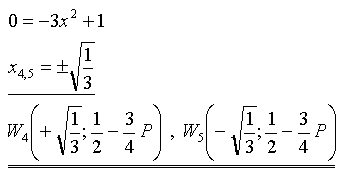|
|
 |
|
|
|
|
|
|
|
gebrochen-rationale Funktionen |
|
|
|
|
|
|
|
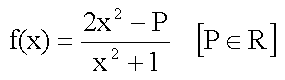 |
|
|
|
Vorsicht - Kurvenschar ! |
|
|
Def.-Bereich, Stetigkeit |
Einschränkend wird zunächst festgelegt, daß
x nur Werte von -4 bis +4 annehmen darf. Auf der Suche nach Unstetigkeitsstellen
betrachten wir zunächst den Nenner und stellen fest, daß dieser
immer positiv ist. Also ist f(x) im gesamten Definitionsbereich stetig.
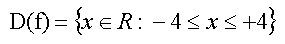 |
|
|
Nullstellen |
Wie wir sehen werden, beeinflußt der Parameter Anzahl und Lage
der Nullstellen:
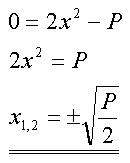
Das bedeutet:
p < 0 ... keine Nullstellen
p = 0 ... eine (doppelte) Nullstelle bei x = 0
p > 0 ... zwei symmetrische Nullstellen |
Randbemerkung:
Die Wurzel aus einer negativen
Zahl läßt sich für Nicht - Mathe - Studenten immer noch
nicht "ziehen". |
|
Extrempunkte
und Nachweis |
Wir berechnen zunächst die erste Ableitung :
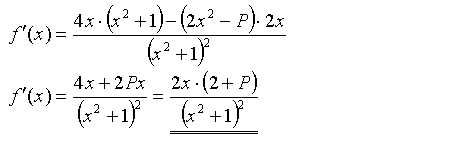
Man erkennt leicht, daß x = 0 eine mögliche Extremstelle
ist.
Der Fall P = -2 sollte eigentlich verboten werden. Im Rahmen einer
Zusatzaufgabe kann man ja mal darüber nachdenken, was es für
Konsequenzen hätte, P auf diesen Wert festzulegen.
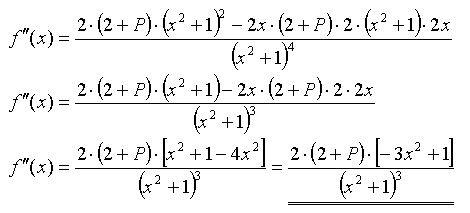
Man sieht leicht, daß f''(0) für P > -2 positiv und sonst
negativ ist. So hätte man es bei P = 1 z.B. mit einem Minimum zu tun,
dessen y-Koordinate von P abhängig ist.
Der dritte bekannte Punkt ist somit (0;-P). |
Randbemerkung:
Auch hier rechnet man mit der Quotientenregel
und untersucht nur den Zähler. Der Nenner ist ja schon erledigt... |
|
Wendepunkte |
Da P = -2 unsinnig ist, können wir uns nun getrost an die Berechnung
der Wendepunkte machen:
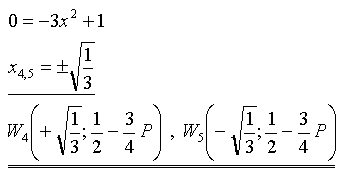
Auf den Nachweis der Wendepunkte wird verzichtet. |
Randbemerkung:
In solch einfachen Fällen
kann man den Rechenweg kurz halten. |
|
Verhalten im Unendlichen |
Das Verhalten von f(x) im Unendlichen wird durch die höchste Potenz
von x in Zähler und Nenner bestimmt. Zähler und Nenner haben
in unserem Beispiel beide den Grad 2, so daß man die anderen Summanden
vernachlässigen kann.
 |
|
|
Graph |
Zur Veranschaulichung der Kurvenschar wurden hier für P die natürlichen
Zahlen von 1 bis 5 vorgegeben. Die rote Kurve ergibt sich bei P = 1.
 |
|
|
|
|
|