gebrochen-rationale Funktionen
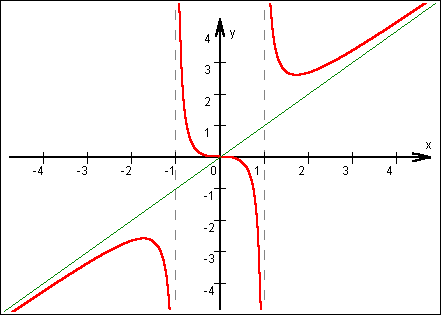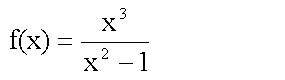
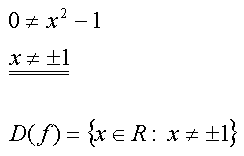
	Def.-Bereich, Stetigkeit	Wie erwartet, ist dazu der Nenner zu untersuchen. Die Funktion hat also zwei Polstellen bei -1 und +1.
	Nullstellen	Eine entsprechende Rechnung kann ich mir sparen. Bei x = 0 hat f(x) mit Sicherheit eine Nullstelle.
	Extrempunkte  und Nachweis	Wir berechnen zunächst die erste Ableitung :  Die mögliche Extremstelle x = 0 stellt sich nach Untersuchung mit der 2. Ableitung nicht als solche heraus. Wieder mal ein Sattelpunkt ?	Randbemerkung: Natürlich rechnet man hier mit der Quotientenregel und untersucht  nur den Zähler. Der Nenner ist ja schon erledigt...
	Wendepunkt und Nachweis	Die weiteren Ableitungen bestätigen die Sattelpunkt - Hypothese.	Randbemerkung: Der ausführliche Rechenweg der dritten Ableitung war mir hier zu lang ...
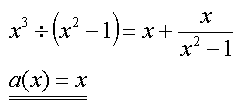
	Verhalten im Unendlichen	Mittels Division schreiben wir den Funktionsterm als Summe : Ergebnis:  f(x) nähert sich im Unendlichen der Asymptote a(x) an.
	Graph	Alle Merkmale gemeinsam ergeben folgendes Bild:

 

Post an mich	Startseite	honich.de