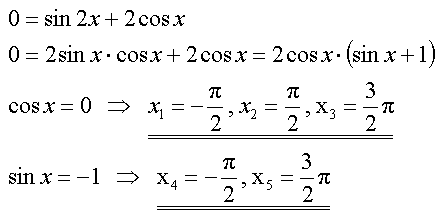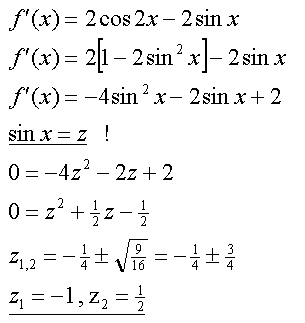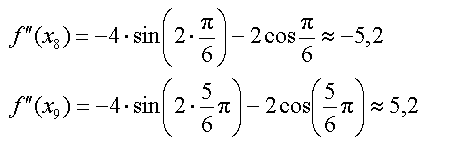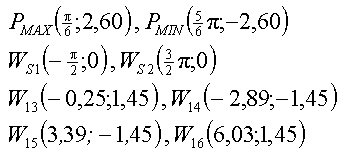|
|
 |
|
|
|
|
|
|
|
trigonometrische Funktionen |
|
|
|
|
|
|
|
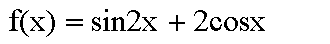 |
|
|
|
Betrachtet man sich diese Funktionsgleichung, liegt die Vermutung nahe,
daß zielgerichtete Berechnungen einen Blick ins Tafelwerk erfordern.
Unter der Überschrift "Beziehungen zwischen den Winkelfunktionen"
findet man dort u.a. folgendes:

Später dazu mehr. |
|
|
|
|
|
|
Def.-Bereich, Stetigkeit |
Da die zugrundeliegenden Funktionen y = sin x und y = cos x beide überall
stetig sind, ist dies auch hier vorauszusetzen. Einschränkend möchte
ich folgenden Definitionsbereich festlegen:
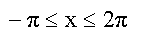 |
|
|
Nullstellen |
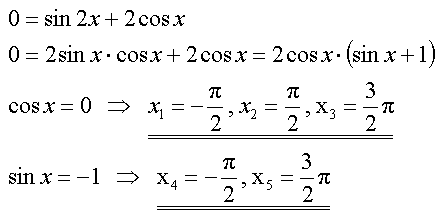 |
Randbemerkung:
Dem aufmerksamen Beobachter ist
nicht entgangen, daß hier bereits die erste der o.g. Beziehungen
angewendet wurde. Somit konnte der Funktionsterm als Produkt geschrieben
werden, um beide Faktoren getrennt zu betrachten. |
|
Extrema |
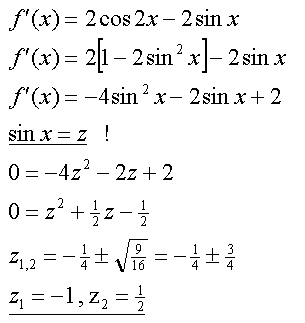 |
Randbemerkung:
Hier nun der zweite Streich. Ansonsten
sieht man, daß das Substitutionsverfahren nicht nur auf symmetrische
Funktionen vierten Grades angewendet werden muß. |
|
|
Da hatten wir also noch einmal die Gelegenheit, das altbekannte Substitutionsverfahren
anzuwenden. Kommen wir nun zur Rücksubstitution:
 |
Randbemerkung:
Bereits bei der Nullstellenberechnung
sind uns einige doppelte Lösungen aufgefallen. Hier finden wir sie
wieder. |
|
Wendepunkte |
Aus Zeitgründen möchte ich zunächst auf den Nachweis
der Extrema verzichten. Erst mal sehen, was uns die Berechnung der Wendepunkte
für Erkenntnisse liefert.
 |
Randbemerkung:
Wieder einmal erweist sich die
Produkt - Schreibweise als überlegen, weil man die Faktoren einzeln
untersuchen kann. |
|
Zusammen- fassung |
Man erkennt zunächst, daß die Lösungen der Gleichung
sin x = -1 keine Extrempunkte, sondern Sattelpunkte liefern. Aber untersuchen
wir zunächst die Lösungen der Gleichung sin x = 0,5 :
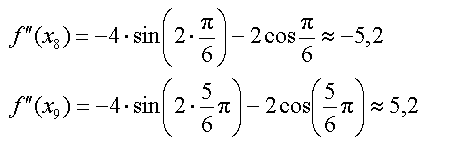
Also gibt es genau zwei Extrempunkte. Auf weitere Nachweise möchte
ich verzichten - schauen wir uns lieber die Lösungen an:
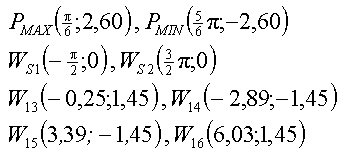 |
|
|
Graph |
Im Definitionsbereich ergibt sich somit folgendes Bild:
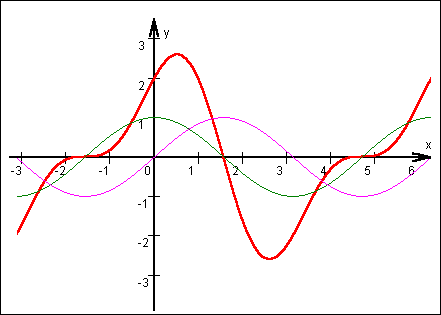 |
Randbemerkung:
Zum Vergleich dienen die Funktionen
sinx und cosx - insbesondere sorgen sie für Klarheit über die
Anzahl der Lösungen trigonometrischer Gleichungen. |