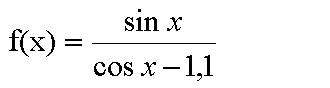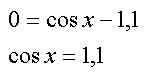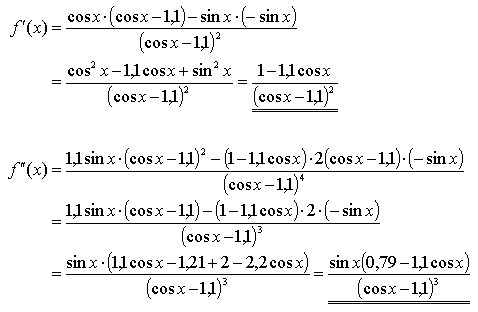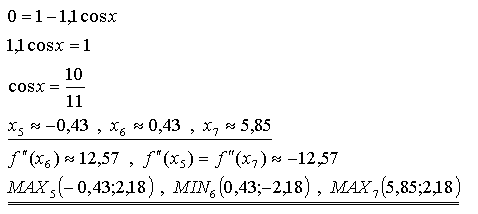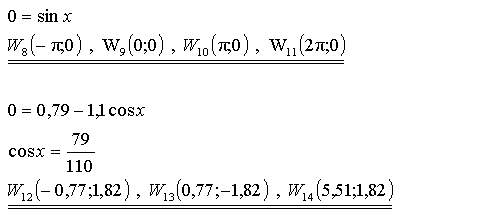trigonometrische Funktionen
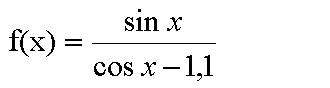		Betrachtet man sich diese Funktionsgleichung, liegt die Vermutung nahe, daß zielgerichtete Berechnungen einen Blick ins Tafelwerk erfordern. Unter der Überschrift "Beziehungen zwischen den Winkelfunktionen" findet man dort u.a. folgendes:  Später dazu mehr.
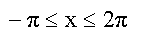
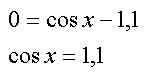
	Def.-Bereich, Stetigkeit	Einschränkend sei der Definitionsbereich begrenzt auf Nun ist die Untersuchung des Nenners erforderlich: Das war's schon - die Cosinusfunktion wächst niemals über 1 hinaus.
	Nullstellen	Der Zähler liefert uns nach kurzer Überlegung folgende Lösungen:
	Ableitungen		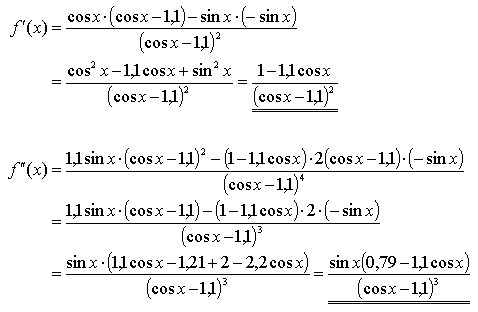Randbemerkung: An dieser Stelle wurde auf die eingangs erwähnte trigonometrische Beziehung zurückgegriffen.
	Extrema	Wir setzen den Zähler der ersten Ableitung gleich Null:	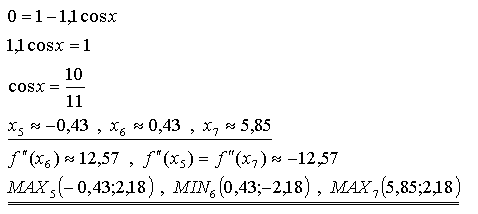Randbemerkung: Die Lösungen deuten auf ein periodisches Verhalten hin.
	Wendepunkte	Der Zähler der zweiten Ableitung ist ein Produkt, und beide Faktoren werden getrennt betrachtet:	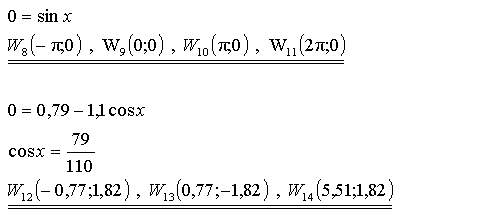Randbemerkung: Wieder einmal erweist sich die Produkt - Schreibweise als überlegen, weil man die Faktoren einzeln untersuchen kann.
	Graph	Im Definitionsbereich ergibt sich somit folgendes Bild:	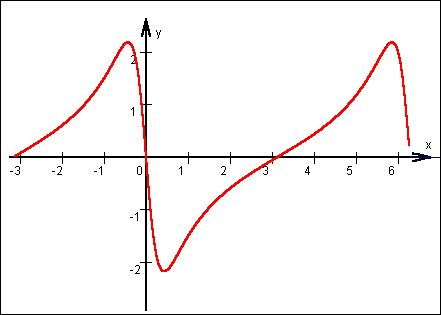Randbemerkung: Die Vermutung mit der Periodizität bestätigt sich. Die Periodenlänge beträgt 2Pi.

 

Post an mich	Startseite	honich.de