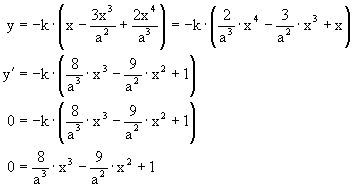
| Lösung des Beispiels: |
Die Gleichung für die neutrale Faser des Trägers ist als Funktion aufzufassen. Zur Berechnung der maximalen Durchbiegung ist die Gleichung abzuleiten :
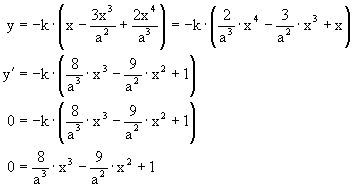
Zur Lösung der so entstandenen Gleichung wird die Länge des Trägers eingesetzt :

Nach intensiver Überlegung findet man bei x1 = 8 eine Lösung dieser Gleichung. Weitere Lösungen sind durch Polynomdivision zu ermitteln :

Welche dieser drei Lösungen ist die Stelle der maximalen Durchbiegung, also ein lokales Minimum ? Wir untersuchen die zweite Ableitung :
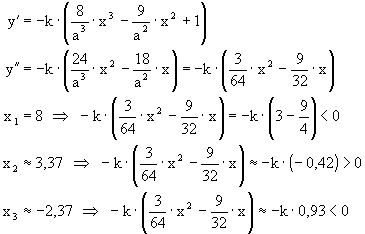
Somit liegt die Stelle der maximalen Durchbiegung
nach unten bei x2 = 3,37 .
Zur Veranschaulichung wird der Funktionsgraph skizziert, wobei man für die Konstante k die Werte 0,5 ; 1 und 2 eingesetzt hat.
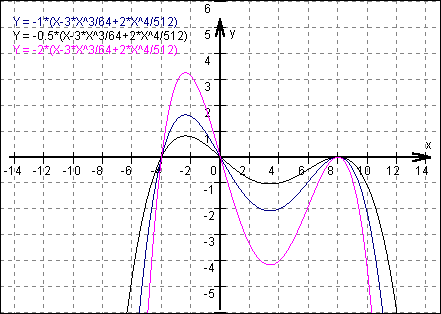
Der in Teilfrage b) beschriebene Auflagepunkt liegt also bei x = -4 . Der vorgegebene Anstieg soll dort 1° betragen, was einem Wert von 0,01745 entspricht. Wir berechnen nun k :
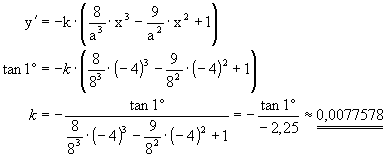
|
|